TUGAS UAS : Pengantar Bahasa dan Otomata (RYAN GESVARY/161021450492/ERESHA/05TPLM003)

TUGAS PENGANTAR BAHASA DAN OTOMATA

Dosen Agus Suharto

Assallamuallaikum wr.wb. Salam sehat dan positif selalu dalam menjalani setiap hidup.

Hari ini saya ingin memaparkan beberapa tugas Pengatar Bahasa dan Otomata dengan pengerjaan tugas meliputi JFLAP dengan metode pengerjaan Grammar.

Berikut penjelasan yang saya buat.

GRAMMAR

Grammar adalah bentuk abstrak yang dapat diterima (accept) untuk membangkitkan suatu kalimat otomata berdasarkan suatu aturan tertentu.

Grammar G didefinisikan sebagai pasangan 4 tuple : V , V , S, dan P, dan dituliskan sebagai G(V , V , S, P), dimana :

V : himpunan  simbol-simbol  terminal  (alfabet) àkamus

V : himpunan simbol-simbol non terminal

T : himpunan simbol terminal

p : himpunan produksi

S : simbol awal (atau simbol start)

Contohnya :

V : {B, R, I, A, N}

T : {v, w}

P : B →vA, B→wR, A→wN, A→vI, A→w, I→w, I→vR, N→vI, N→wN, N→B, R→R, R→vA, R→w

S : B

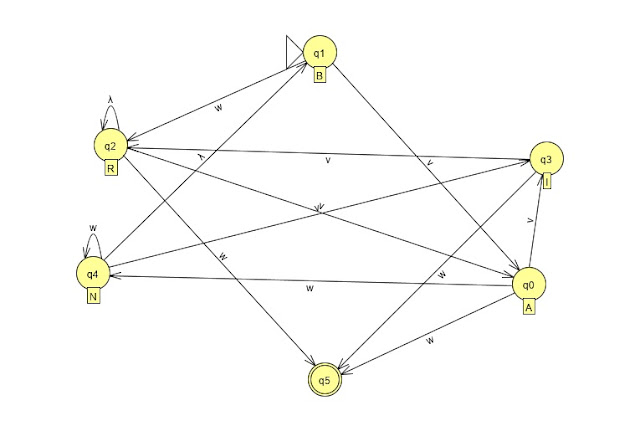
Kemudian kita buat di Aplikasi Jflap dengan grammar, kita masukan himpunan produksinya ke dalam grammar tersebut kemudian kita pilih convert to FA dan hasilnya akan seperti ini :

Setelah sesuai hasilnya kita test input bisa dengan Brute Parser atau Multiple Run

Kali ini kita akan mencoba input dengan multiple run :

Dan hasilnya :

wvvw             : Accept

vwvw             : Accept

vw                  : Accept

wvw               : Accept

ww                 : Accept

vvvw              : Accept

wwwwvw      : Reject

FSA

Finite Automata adalah model matematika sistem dengan masukan dan keluaran diskrit. Finite State Automata adalah model matematika yang dapat menerima inputan dan mengeluarkan output. Memiliki state berhingga banyaknya dan dapat berpindah dari satu ke yang lainnya sesuai dengan inputan dan fungsi transisi.

Finite State Automata dinyatakan oleh pasangan 5 tuple, yaitu:
M=(Q , Σ , δ , S , F )
Q = himpunan state
Σ = himpunan simbol input
δ = fungsi transisi δ : Q × Σ
S = state awal / initial state , S ∈ Q
F = state akhir, F ⊆ Q

Deskripsi

§  M = (Q, ∑, δ, S, F),

§  Q = {q0,q1, q2, q3, q4,q5}

§  ∑ = {0,1}

§  S = q0

§  F = {q5}

§  δ

Q	0	1
q0	q1	q2
q1	q2	q3
q2	q3	-
q3	-	q4
q4	-	q4
q5	q4	-

Berdasarkan hasil di atas maka akan didapat hasil sebagai berikut :

§  View Trace

1.      Run inputs dari 10101 menyatakan Accept

       

2.      Run inputs dari 1010101 menyatakan Accept

3.    Run inputs dari 101101 menyatakan Reject

Sekian tugas dari saya, bila ada kesalahan dalam pengerjaan dan kesamaan dalam penulisan kata mohon dikoreksi. Wassallamuallaikum wr.wb.